1. 若$2x^{4}-3x^{3}+ax^{2}+7x+b$能被$x^{2}+x - 2$整除,则$a:b$的值是(
A.$-2$
B.$-12$
C.$6$
D.$4$
A
)A.$-2$
B.$-12$
C.$6$
D.$4$
答案:1. A 点拨:由题意可设$2x^{4}-3x^{3}+ax^{2}+7x+b=(x^{2}+x - 2)(2x^{2}+mx + n)$,因为$(x^{2}+x - 2)(2x^{2}+mx + n)=2x^{4}+mx^{3}+nx^{2}+2x^{3}+mx^{2}+nx - 4x^{2}-2mx - 2n=2x^{4}+(m + 2)x^{3}+(n + m - 4)x^{2}+(n - 2m)x - 2n$,所以$2x^{4}-3x^{3}+ax^{2}+7x+b=2x^{4}+(m + 2)x^{3}+(n + m - 4)x^{2}+(n - 2m)x - 2n$,所以$\begin{cases}m + 2=-3,\ + m - 4=a,\ 2m=7,\\-2n=b,\end{cases}$解得$\begin{cases}m=-5,\ =-3,\\a=-12,\\b=6,\end{cases}$所以$a:b=(-12):6=-2$.
2. 已知$x^{2}+3x - 5 = 0$,则$x(x + 1)(x + 2)(x + 3)$的值是
35
。答案:2. 35 点拨: 因为 $ x^{2}+3x - 5=0 $,所以 $ x^{2}+3x=5 $,所以原式 $ =[x(x + 3)][(x + 1)(x + 2)]=(x^{2}+3x)(x^{2}+3x + 2)=5×(5 + 2)=5×7=35 $。
3. 我国古代数学的许多发现都曾位居世界前列,“杨辉三角”就是其中一例,如图所示为这个“三角形”的构造法则:两腰上的数都是$1$,其余每个数均为其上方左右两数之和,它给出了$(a + b)^{n}$($n$为正整数)的展开式(按$a$的次数由大到小的顺序排列)的系数规律。例如,在“三角形”中,第三行的三个数$1$,$2$,$1$,恰好对应$(a + b)^{2}=a^{2}+2ab + b^{2}$展开式中的系数;第四行的四个数$1$,$3$,$3$,$1$,恰好对应$(a + b)^{3}=a^{3}+3a^{2}b + 3ab^{2}+b^{3}$展开式中的系数。
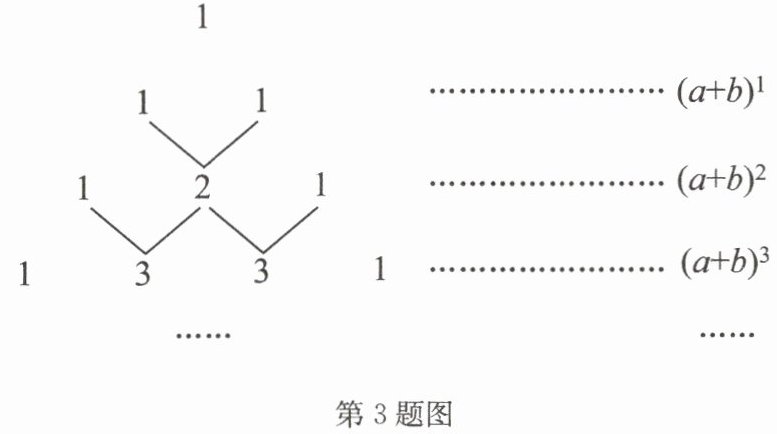
(1)根据上面的规律,写出$(a + b)^{4}$的展开式;
(2)利用上面的规律计算:$2^{5}-5×2^{4}+10×2^{3}-10×2^{2}+5×2 - 1$;
(3)$(a + b)^{n}$的展开式的系数和为
(4)运用:若今天是星期三,经过$2024^{2024}$天后是星期

(1)根据上面的规律,写出$(a + b)^{4}$的展开式;
(2)利用上面的规律计算:$2^{5}-5×2^{4}+10×2^{3}-10×2^{2}+5×2 - 1$;
(3)$(a + b)^{n}$的展开式的系数和为
$2^{n}$
;(4)运用:若今天是星期三,经过$2024^{2024}$天后是星期
四
。答案:3. (1) 解: $ (a + b)^{4}=a^{4}+4a^{3}b+6a^{2}b^{2}+4ab^{3}+b^{4} $。
(2) 解: $ 2^{5}-5×2^{4}+10×2^{3}-10×2^{2}+5×2 - 1=(2 - 1)^{5}=1^{5}=1 $。
(3) $ 2^{n} $ 点拨: 由展开式知,当 $ n = 1 $ 时,系数和为 $ 1 + 1=2=2^{1} $;当 $ n = 2 $ 时,系数和为 $ 1 + 2 + 1=4=2^{2} $;当 $ n = 3 $ 时,系数和为 $ 1 + 3 + 3 + 1=8=2^{3} $;当 $ n = 4 $ 时,系数和为 $ 1 + 4 + 6 + 4 + 1=16=2^{4} $,…,由此可得 $ (a + b)^{n} $ 的展开式的系数和为 $ 2^{n} $。
(4) 四 点拨: $ 2024^{2024}=(2023 + 1)^{2024}=2023^{2024}+2024×2023^{2023}+…+2024×2023 + 1 $,因为 $ 2023÷7 = 289 $,所以 $ 2024^{2024}÷7 $ 的余数为 1,故若今天是星期三,经过 $ 2024^{2024} $ 天后是星期四。
(2) 解: $ 2^{5}-5×2^{4}+10×2^{3}-10×2^{2}+5×2 - 1=(2 - 1)^{5}=1^{5}=1 $。
(3) $ 2^{n} $ 点拨: 由展开式知,当 $ n = 1 $ 时,系数和为 $ 1 + 1=2=2^{1} $;当 $ n = 2 $ 时,系数和为 $ 1 + 2 + 1=4=2^{2} $;当 $ n = 3 $ 时,系数和为 $ 1 + 3 + 3 + 1=8=2^{3} $;当 $ n = 4 $ 时,系数和为 $ 1 + 4 + 6 + 4 + 1=16=2^{4} $,…,由此可得 $ (a + b)^{n} $ 的展开式的系数和为 $ 2^{n} $。
(4) 四 点拨: $ 2024^{2024}=(2023 + 1)^{2024}=2023^{2024}+2024×2023^{2023}+…+2024×2023 + 1 $,因为 $ 2023÷7 = 289 $,所以 $ 2024^{2024}÷7 $ 的余数为 1,故若今天是星期三,经过 $ 2024^{2024} $ 天后是星期四。